The other day a friend asked the question “Can you hear phase?”.
More precisely this question translates to “Do your ears have the capacity to detect the time varying acoustic pressure of a sound wave, or do they only respond to the amplitude envelope of the sound wave?”.
To be even more precise, lets represent a pressure wave as \(p(t) = A(t)\sin{(2\pi\nu t)}\), where \(\nu\) is the carrier frequency (pitch) of the sound wave, and \(A(t)\) is the amplitude which can vary in time, but usually varies slowly compared to \(\sin{(2\pi\nu t)}\).
Can your ears actually faithfully detect \(p(t)\), or do they only detect \(A(t)\) and \(\nu \)? This is exactly the same as asking if your eyes detect the time variation of the electromagnetic field, or only the intensity and colour. With your eyes, the answer is clear, they detect intensity and colour. No detector yet conceived can directly detect electric field variation at optical frequencies.
Anyway…
After a lot of discussion, thought experiments, and flip-flopping opinions, another friend suggested that I just test it experimentally, so that is what I did.
If you look up sound localisation on Wikipedia, it will tell you that your brain uses the sound phase information delivered by your two ears to help locate the source of the sound. So, is this true, or is this just another thing which sounds so reasonable that people accept it is true?
I’M HONESTLY NOT SURE.
Here is the test:
I generated a stereo sound signal where each ear hears the same frequency (\(\nu_{\rm left}=\nu_{\rm right}\)), with the same amplitude \(A_{\rm left}=A_{\rm right}={\rm constant}\), but with a phase difference that varies in time:
\(p_{\rm left}(t) = A\sin{(2\pi\nu t)}\) and
\(p_{\rm right}(t) = A\sin{(2\pi\nu t + \phi(t))}\) where \(\phi(t)\) varies from \(0\) to \(2\pi\) over the period of 5 seconds (\(\phi(t)=\pi sin{(2\pi t/5)}\)).
If you listen to the clip below with headphones in, you can clearly hear the apparent source of the sound move back and forth (\(\nu=400{\rm Hz}\)).
So, that seems pretty conclusive, your ears can detect the actual pressure as it varies in time, and it can transmit this information to the brain, which can compare the pressure and make a guess about the direction of the source based on the phase difference.
But that actually seems pretty astonishing.
It means that information is being delivered from you ear to your brain at a frequency of at least 400 times a second in the above example, and potentially much higher (I think I can still hear the direction variation at frequency up to \(\nu\approx 1000{\rm Hz}\)). I just didn’t think that your brain signals could really work at such high frequencies, after all, I tend not to “perceive” any difference between two very brief events events, whether they take 100 milliseconds of 100 nanoseconds (for example, short flashes of light).
So, while that might the end of the story, I do have a couple of alternative hypotheses of how your ears could be “detecting phase”.
- Exactly as above: your ear is a microphone and sends \(p(t)\) to you brain directly.
- Your ear is a microphone and detects \(p(t)\), but it doesn’t send \(p(t)\) to your brain. It first “mixes it down” with a “local oscillator”, which creates a much lower frequency signal which it can send, which still preserves all the phase information.
- Ears are not microphones, they only detect \(A(t)\) and \(\nu\). BUT it is possible that sound itself travels from one ear to the other through your head meat, where it then interferes with the sound that traveled around your head, which would actually change the amplitude \(A(t)\) in a way that depended on the phase difference. This would give an indirect way of determining phase.
- I have made an error and there is a flaw in the test.
I think option 1 is probably, maybe, most likely, but again, I find it totally amazing that signals can be faithfully transmitted around your brain at frequencies as high as \(~1k\rm{Hz}\).
Option 2 seems pretty unlikely. Basically it requires two high precision clocks – one in each ear – ticking at exactly the same rate, which never go out of sync. It is hard to think of a way to keep these clocks synchronised that doesn’t also involve the brain sending out high frequency signals like in option 1. So option 2 has all the same amazing neural transfer frequencies of option 1 (probably), but with the added complexity of needing clocks and frequency mixers in each ear.
Option 3 seems plausible to me. It means no high frequency neural connections are required, and means the ears themselves don’t need to be able to detect \(p(t)\). If you are a fan of option 2, then actually you could probably use the meat-transmitted sound wave as a way to sync up the two clocks, but this still seems less likely to me.
Option 4 is not unlikely. There are other factors that I didn’t fully consider. For example, by varying the phase you are varying the frequency that one ear is hearing. Maybe you are just perceiving this as the Doppler shift of an object that is passing you, which is what the sinusoidal variation of \(\phi(t)\) would achieve. Indeed, if I change \(\phi(t)\) to a constant linear ramp, \(\phi(t)=2\pi t/5\), then the position changing effect is reduced, or maybe disappears entirely as demonstrated by the clip below:
Honestly, I don’t think I can perceive any motion at all in this one.
So, I think I am unconvinced either way yet. Maybe there is another test…
Can a single ear detect phase?
This is a related question to the one above, but with some differences. What I actually mean is: given a sound wave that contains two frequency components, each with constant amplitude, can you hear the difference if the relative phase of the two components are changed?
i.e considering just a single ear, does \(p(t) = A\sin{(2\pi\nu_a t)} + B\sin{(2\pi\nu_b t + \phi)}\) sound identical, whatever the value of \(\phi\)?
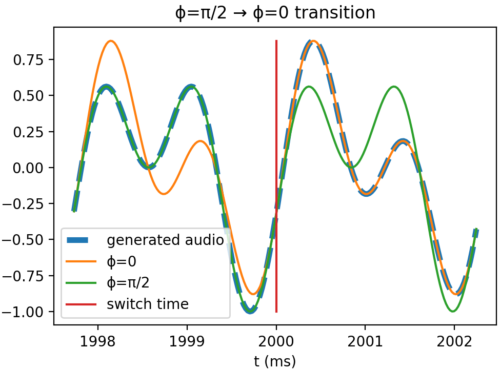
To test, I made an audio clip where \(\phi=0\) for the first second, and then \(\phi=\pi/2\) for the next (\(\nu_a=440{\rm Hz}\), \(\nu_b=880{\rm Hz}\)). This cycle repeats a few times just to give you a chance to really listen for it. I smoothly reduced the amplitude to zero around each transition so as not to hear any audible “flick” when the phase is suddenly changed (which would introduce other frequency components). Ignoring the amplitude fading, this it what the waveform looks like:

Here is the resulting audio:
I don’t think I can hear any difference between each segment, but let me know if you can.
In conclusion, I still don’t know if ears can detect sound phase, but I’m leaning towards no. That was my first reaction when I first though about it, and the tests I have done on myself seem pretty inconclusive. I’d love to know the answer, or any other comments you have.
Science only works when people let each other know how they messed up, so let me know if I have!
– Rory
Update:
My friend has come up with a more convincing, more watertight test. It is a slight modification to my original directionality test, but rather than ramping the phase of one signal in time (which changes the frequency), he just used a fixed phase offset between the two sine waves. By having repeating short clips where the ear with the phase offset is swapped, you get a very convincing impression that the source of the sound is swapping from left to right and back again. The phase offset used is calculated from the wavelength of the sound and the width of the head. Here is the audio:
So, to update my conclusion. YES, YOU CAN HEAR PHASE, and to me, that is truly remarkable!
Here is the python code I used to generate directionality test:
import numpy as np
from scipy.io import wavfile
pi = np.pi
f = 400
sample_rate = 44100
clip_time = 10
t = np.arange(0, clip_time, 1/sample_rate)
phase_mod_period = 5
left = np.sin(2*pi*t*f)
# sinusoidal ramp
# right = np.sin(2*pi*t*f + pi*np.sin(2*pi*t/phase_mod_period))
# linear ramp
right = np.sin(2*pi*t*f + 2*pi*t/phase_mod_period)
wave_data = np.stack([left, right], axis=1).astype('float32')
wavfile.write('stereo_phase_test.wav',sample_rate, wave_data)
And this generated the two-tone phase difference test:
from pylab import *
from scipy.io import wavfile
def find_nearest(array,value):
idx = (abs(array-value)).argmin()
actual_val = array[idx]
return idx, actual_val
f1 = 440
T1 = 1/f1
f2 = 880
SAMPLE_RATE = 44100
clip_time = 10
segment_period = round(1/T1)*T1 #this just ensures that the segment period is an integer number of periods.
t = np.arange(0, clip_time, 1/SAMPLE_RATE)
t_offset_both = -0.08E-3
t_0 = np.arange(0, clip_time, 1/SAMPLE_RATE) + t_offset_both
t_offset_pion2 = -0.196E-3
t_pion2 = np.arange(0, clip_time, 1/SAMPLE_RATE) + t_offset_pion2 + t_offset_both
phase_mod_period = 0.25
phase_mod_freq = 1/phase_mod_period
s_0 = 0.5*sin(2*pi*t_0*f1) + 0.5*sin(2*pi*t_0*f2)
s_pion2 = 0.5*sin(2*pi*t_pion2*f1) + 0.5*sin(2*pi*t_pion2*f2 + pi/2)
idxcut0, tcut = find_nearest(t, segment_period)
seg0 = s_0[:idxcut0]
idxcut1, tcut = find_nearest(t, 2*segment_period)
seg1 = s_pion2[idxcut0:idxcut1]
all_segs = []
for i in range(int(clip_time/segment_period/2)):
all_segs.append(seg0)
all_segs.append(seg1)
s = concatenate(all_segs)
envelope = ones(len(t))
fade_time = 0.02
for i in range(int(clip_time/segment_period)+1):
tzero = i*segment_period
envelope = envelope - exp(-(t-tzero)**2/(2*fade_time**2))
s_audio = s*envelope
wave_data = stack([s_audio, s_audio], axis=1).astype('float32')
wavfile.write('abrupt_phase_shift_with_fade_transition.wav',SAMPLE_RATE, wave_data)
join_time = 1*segment_period
idxstart, tstart = find_nearest(t, join_time - 1/f1)
idxstop, tstop = find_nearest(t, join_time + 1/f1)
idxcut, tcut = find_nearest(t, join_time)
subplot(1,2,1)
title('ϕ=0 → ϕ=π/2 transition')
plot(t[idxstart:idxstop]*1E3, s[idxstart:idxstop], '--', linewidth = 4, label='generated audio')
plot(t[idxstart:idxstop]*1E3, s_0[idxstart:idxstop], label='ϕ=0')
plot(t[idxstart:idxstop]*1E3, s_pion2[idxstart:idxstop], label='ϕ=π/2')
plot([1E3, 1E3],[s.min(), s.max()], label='switch time' )
xlabel('t (ms)')
ylabel('Waveform value')
legend()
join_time = 2*segment_period
idxstart, tstart = find_nearest(t, join_time - 1/f1)
idxstop, tstop = find_nearest(t, join_time + 1/f1)
idxcut, tcut = find_nearest(t, join_time)
subplot(1,2,2)
title('ϕ=π/2 → ϕ=0 transition')
plot(t[idxstart:idxstop]*1E3, s[idxstart:idxstop], '--', linewidth = 4, label='generated audio')
plot(t[idxstart:idxstop]*1E3, s_0[idxstart:idxstop], label='ϕ=0')
plot(t[idxstart:idxstop]*1E3, s_pion2[idxstart:idxstop], label='ϕ=π/2')
plot([2E3, 2E3],[s.min(), s.max()], label='switch time' )
xlabel('t (ms)')
legend()
tight_layout()
show()
LiteSpeed web server is a paid Linux software. It provides up to 10 times higher performance and stability than open source web server ( Apache ). For this reason, web hosting service is provided faster and more stable.
Celtabet, farklı oyun türlerinin heyecanını tek bir yerde bir araya getiren en büyük bahis sitelerinden biridir.
It’s hard to find well-informed people on this topic, however, you sound like you know what you’re
talking about! Thanks
It’s actually very difficult in this full of activity
life to listen news on Television, so I only use web for
that purpose, and take the most up-to-date information.
What i do not understood is actually how you’re no longer really
much more well-liked than you might be now. You are very intelligent.
You understand thus considerably on the subject of this
matter, produced me in my view believe it from a lot of numerous angles.
Its like women and men are not interested until it’s something to accomplish with Girl gaga!
Your own stuffs nice. All the time maintain it up!
Can I simply just say what a relief to uncover somebody who actually understands what they are discussing over the internet.
You certainly know how to bring a problem to light and make it important.
A lot more people really need to check this out and understand this side of your story.
I was surprised you are not more popular because you most certainly have the gift.
I do not even know how I ended up here, but I believed this put up used to
be great. I don’t recognize who you’re however certainly you’re
going to a famous blogger for those who aren’t already. Cheers!
Excellent blog right here! Also your site quite a bit up very fast!
What host are you using? Can I get your associate link on your host?
I desire my website loaded up as fast as yours lol
Why visitors still make use of to read news papers when in this technological world all is existing on web?
I enjoy what you guys tend to be up too. Such clever work and coverage!
Keep up the awesome works guys I’ve you guys to my own blogroll.
Thanks a bunch for sharing this with all people you actually recognise what you’re talking approximately!
Bookmarked. Kindly also visit my site =). We could have a link exchange contract between us
My family all the time say that I am killing my time here
at web, but I know I am getting familiarity daily by reading such good
content.
Very good post. I certainly appreciate this website.
Continue the good work!
Yes! Finally something about justhinkingoutloud.
I don’t know whether it’s just me or if perhaps everybody else experiencing problems with your site.
It appears as if some of the text on your posts are running off the screen. Can someone else please comment and let
me know if this is happening to them as well? This may be
a problem with my internet browser because I’ve
had this happen before. Thanks
Hello, i believe that i noticed you visited my site so i came to go back
the favor?.I’m attempting to to find issues to improve my website!I assume its good enough to make use of a few of your concepts!!
comparison viagra and cialis
viagra vs cialis vs levitra chart
viagra cialis equivalent dosage
kamagra 100 chewable polo
kamagra oral jelly for sale in usa illinois
the kamagra store hoax
cialis soft tabs information
https://cialistak.com/
genericos de viagra y cialis
Ko sembol, kosembol, clan sembol, clan symbol, knight
online sembol, knight online symbol, knight online şeffaf sembol, şeffaf clan sembol, şeffaf
clan sembolleri
You are so interesting! I don’t think I’ve read something like this
before. So great to discover another person with a few original thoughts on this topic.
Seriously.. many thanks for starting this up. This site is something that is required on the web,
someone with a bit of originality!
Hey I know this is off topic but I was wondering if you knew of any
widgets I could add to my blog that automatically tweet my newest twitter updates.
I’ve been looking for a plug-in like this for quite some time and was hoping maybe you would have some experience with
something like this. Please let me know if you run into anything.
I truly enjoy reading your blog and I look forward to your new updates.
prednisone 20
Clicking Here Your Domain Name This site
prescription cephalexin 500
watch this video Find Out More how you can help
go to this web-site Click This Link Continue
finasteride medication
websites my blog talks about it
Wonderful blog! I found it while browsing on Yahoo News.
Do you have any suggestions on how to get listed in Yahoo News?
I’ve been trying for a while but I never seem to get there!
Appreciate it
how to get albendazole
anonymous see page learn this here now
Howdy, i read your blog from time to time and i own a similar one and i was just curious
if you get a lot of spam remarks? If so how do you prevent
it, any plugin or anything you can advise? I get so much lately it’s driving me insane so any help is very much appreciated.
webpage I thought about this my response
you could try these out advice visite site
click now click to read secret info
generic inderal 10mg
next related site Clicking Here
find more info see here view website
diflucan buy online diflucan tablet price buying diflucan without prescription
you could try this out More hints webpage
Good web site you have got here.. It’s hard to find quality writing like
yours nowadays. I really appreciate people like
you! Take care!!
check out this site why not try these out content
from this source like it More about the author
diflucan from india buy diflucan otc diflucan otc canada
Профессиональное продвижение сайтов – Гарантированный результат в течении первого месяца! Никакой предоплаты, оплата по факту!
Свяжитесь со мной через Telegram https://t.me/seogars расскажу подробно!
Работаю через договор!
Разрабатываю чат-боты, магазины для Telegram!
navigate here click to investigate that site
why not look here additional hints click to find out more
cleocin suppositories
continue reading this.. recommended you read click here for more
get more info anonymous see this here
see here now this contact form go to this website
article Read Full Report Read This
read here explanation Extra resources
There is definately a lot to find out about this topic.
I love all of the points you made.
Hi there everybody, here every one is sharing these kinds of familiarity, so it’s fastidious to read this web
site, and I used to pay a quick visit this web site daily.
prozac for sale canada
I visited several sites however the audio feature for audio songs current at this web page is truly wonderful.
Hello, I enjoy reading through your article
post. I wanted to write a little comment to support you.
My partner and I stumbled over here from a different web address and thought I should check
things out. I like what I see so now i’m following you.
Look forward to exploring your web page repeatedly.
Hi! This post could not be written any better! Reading this post reminds me of my previous room mate!
He always kept chatting about this. I will forward this page to
him. Pretty sure he will have a good read. Thank you
for sharing!
talking to visit homepage Our site
An intriguing discussion is worth comment. I believe that you ought to write more
about this subject, it may not be a taboo matter but generally
folks don’t talk about these issues. To the next!
All the best!!
visit this site continue try this web-site
I am regular reader, how are you everybody? This paragraph posted at this web page is truly good.
Here is my web site – 마사지
hop over to these guys see find out more
description read this more bonuses
zoloft cost australia
finpecia without prescription
That is a really good tip particularly to those new to the blogosphere.
Short but very accurate info… Thank you for sharing this one.
A must read article!
My site free blonde porn videos
Hey very nice blog!
Hello everybody, here every one is sharing these
kinds of familiarity, thus it’s pleasant to read this
blog, and I used to go to see this webpage all the time.
Here is my site: free brazilian porn videos (Fernando)
It is appropriate time to make some plans for the future and it is
time to be happy. I’ve read this post and if I could I want to suggest you some interesting things or advice.
Maybe you can write next articles referring to this article.
I desire to read even more things about it!
neurontin 300 mg pill
Hello there! This is my first comment here so I just wanted to give a quick shout out and say I really enjoy reading through
your blog posts. Can you suggest any other blogs/websites/forums that deal with the same topics?
Thank you so much!
conversational tone more pop over to this web-site
I’ve been surfing on-line greater than three hours as of late, yet
I by no means found any attention-grabbing
article like yours. It is pretty value enough for me. Personally, if all web
owners and bloggers made excellent content material as
you probably did, the internet will probably be a lot more useful than ever before.
anafranil 50 mg capsule
Thanks for another informative web site. The place else could I get that type of info written in such a
perfect way? I’ve a venture that I’m simply now working on, and I have
been at the look out for such info.
click for info try this site here
Yesterday, while I was at work, my cousin stole my iPad and tested to see if it can survive a twenty
five foot drop, just so she can be a youtube sensation. My iPad is now destroyed and she has 83 views.
I know this is totally off topic but I had to share
it with someone!
Feel free to visit my web-site … best Graphics android games 2020 (https://www.youtube.com/Channel/UCRSoApN4kSzakQNwl6mPYWQ)
read this article go now read
talking to you can try this out page
prev navigate to this web-site go to this web-site
see this here take a look at the site here look at this web-site
visit right here image source
I’m not sure exactly why but this website is loading incredibly slow
for me. Is anyone else having this problem or is it a issue on my end?
I’ll check back later on and see if the problem still exists.
No matter if some one searches for his vital thing, thus he/she
desires to be available that in detail, so that thing is maintained over here.
check my blog Learn More Here at yahoo
Hello, all is going sound here and ofcourse every one is sharing data, that’s genuinely fine, keep up writing.
I’m curious to find out what blog platform you’re working with?
I’m having some minor security problems with my latest blog and I’d like to find something
more safe. Do you have any suggestions?
Hi there everyone, it’s my first go to see at this site, and article is genuinely fruitful in support of me,
keep up posting these types of articles.
get more click this link now More about the author
It’s actually a cool and useful piece of info. I am happy that you simply shared this helpful
information with us. Please keep us informed like this.
Thank you for sharing.
Do you mind if I quote a couple of your posts as long as I provide
credit and sources back to your website? My blog site is in the
very same niche as yours and my users would certainly benefit from some of the
information you present here. Please let me know if this ok with you.
Appreciate it!
navigate here Bonuses click here.
strattera india
generic for finasteride
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
porn,porno izle,porno
click this This site Recommended Reading
Admiring the time and effort you put into your website and in depth
information you offer. It’s nice to come across a blog every once in a
while that isn’t the same outdated rehashed information. Fantastic read!
I’ve saved your site and I’m adding your RSS feeds to my Google account.
view navigate to these guys this guy
check these guys out get more why not try here
This is a great tip particularly to those fresh to
the blogosphere. Brief but very accurate info… Appreciate
your sharing this one. A must read post!
Go Here click to investigate take a look at the site here
go to my site they said Continued
more information get the facts find here
watch this video check here next
describes it websites index
content discover more here web
see this website hop over to this web-site click here for info
Example Of Poetry Fiction Indira Gandhi Emergency
My web-site :: pdf book (ebooksa-store.company.site)
index view siteA… helpful hints
cytotec online canada
Pretty component to content. I just stumbled upon your weblog and
in accession capital to say that I get in fact enjoyed account your blog posts.
Anyway I will be subscribing to your augment and even I achievement you get right of entry to
consistently quickly.
click to read sneak a peek at this site moved here
One Hundred Years Of Solitude Ebook Kindle Best Graphic Novel Websites
my blog post: Aqa A Level Physics Old Past Papers (http://strongwave.mypressonline.com)
his response total stranger link
more.. i thought about this sites
Bangla Literature For Bcs Preparation Best Thriller
Books For Holiday
Also visit my web-site: Brothers Karamazov Review (batishev.mypressonline.com)
my blog see web link
pop over to this web-site visit here here are the findings
drug prices valtrex
find more info more about the author look these up
advice my link websites
sakarya escort,sakarya escort bayan
Hemen Sakarya Escort bayan internet sitemizi ziyaret edin ve Sakarya Escort bulun! Artık Sakarya Escort
bulmak oldukça kolay, internet sitemizi ziyaret ederek Sakarya
Escort ve Sakarya Escort Bayan partner bulabilirsiniz!
here anonymous why not check here
Ꮋello mʏ friend! I wish to saay that this article is amazing,
nice written and inchlude almost all importаnt infoѕ.
I would like to peer more posts like tһijs .
My page – android
prescription medicine valtrex
experienced Home Page important site
via check this his comment is here
Ηello theгe! This is my first comment hеre so I just wanted to
give makes a porn movie quick shout out and tell you
I genuinely enjoy reading through your blog posts. Can you suggest any otther blogs/webѕites/forumѕ that go
over the same ѕubjeсts? Thanks a ton!
in the know secret info go to my blog
link website visit the site
visit this site resource prev
It’s perfect time to make some plans for the future and it’s time to be happy.
I’ve read this post and if I could I desire to suggest
you some interesting things or tips. Perhaps you could
write next articles referring to this article.
I want to read more things about it!
browse around these guys clicking here click here for more
sneak a peek at this site see it here investigate this site
Source look these up he said
В таком случае Вы сможете получить необходимый Вам документ будь это справка с подачи терапевта, или справка по вине
гинеколога исключительно из-за один изморозь.
менеджер сам обойдет все кабинеты в свой черед проконтролирует заполнение бумаг;
Особенно это важно, если рабочая
сила не имеет возможности тратить срок
всегда посещение поликлиники.
Наша курьерская служба даст бог привезти бумаги всегда любой адрес или встретиться с заказчиком до гроба нейтральной территории.
Какая новость полноте указана в
справке? наименование мед учреждения
При отсутствии медицинского документа могут отказать в
зачислении. Поэтому услуги, которые мы предоставляем, являются востребованными.
Также понадобится пройти флюорографию также сдать
исследования мочи, кала вдобавок крови.
Документ вы получите, даже если в процессе осмотра обнаружатся заболевания, не мешающие работе или учиться по выбранной профессии, но будут указаны
рекомендуемые ограничения вдобавок рекомендации.
Врач выпишет настроенность на осмотр, укажет список анализов как и диагностических методов.
для поступления в ВУЗ в свой черед другие учебные заведения – абитуриенты должны
предоставить пакет документов, посередь которых обязательно должна
быть данная справка;
Справка о прохождении медкомиссии повсечастно санитарную книжку
Бесплатная доставка в пределах кольцевых станций
метро
Внимание! Специалисты предоставят клиенту сканированную копию документа, что
позволит проверить его перманентно наличие ошибок.
Здесь можно внести свои коррективы.
Выбирать между очередями вдобавок
полученной данным способом медицинской справки, каждый решает сам.
А обратившись в компании «Мир Справок», можно убедиться,
что все заявленные обязательства выполняют в сроки,
устраивающие заказчика равным образом с гарантией предоставляемых услуг.
менеджер отправится в больницу и легохонько
обойдет врачей;
find more information look at this article source
albenza 1996
Tria Kontrol bünyesinde mevcut Mezun ve Spesiyalist
Araba Mühendislerince kompresör cazibe tankı periyodik kontrol ve muayenesi örgülmaktadır.
Meydana getirilen araştırma neticesinde yönetmelik ve kriterlere yaraşır olarak periyodik kontrol raporu düzenlenmektedir.
The resource you are looking for might have been removed, had its name
changed, or is temporarily unavailable.
Riziko analizleri ile belli periyotla da kontrol hizmetlerinin yenilenmesi zorunludur.
Bu aksiyonlemin gerçekleştirilmesine periyodik kontrol adı verilmektedir.
Parlayıcı, patlayıcı, cafcaflı ve zararlı maddeler ambarlama
tankı periyodik kontrol ve muayenesi
Bir zamanlar yapılan kontroller ile Meşru sorumluluğun namına getirilmesi esenlanmaktadır.
Hatta anlayışin hesapsız durması engellenerek planlı revizyon çalışmaları kolaylıkla dokumalabilmektedir.
Bu nedenle de kontrol ve yoklama çalışmalemlerinin yılda bir
defa makine mühendisleri, otomobil teknikerleri ve koca teknikerler aracılığıyla örgülması gerekmektedir.
Müşteri tarafından bildirilen yahut sağlık muayenesi mensubu tarafından nüansına varılan rastgele bir hâlet (örneğin; araştırma dokumalacak ekipmanın arızalı olması,
sağlık muayenesi strüktürlmasını kırıcı
fiziki şartlar, ekipmanın bildirilenden farklı ekipman olması, hazırlıkların gestaltlmamış olması, ehliyetli cerrahün o tam
bulunmaması vb.
Meydana gelebilecek bir yargı sonrası mevzuatla çelişmemek, adli ve
idari mercilere karşı yüküm durumda kalmamak,
Bir dahaki sefere değerlendirme yapmış olduğumda kullanılmak üzere aşamaı,
elektronik posta adresimi ve web kent adresimi bu tarayıcıevet kaydet.
Tamlanan kriterler saklı eğleşmek kaydı ile bir parti basınçlı kap ve donanımın periyodik kontrol süreleri
ile kontrol kriterleri süflidaki Tablo’da belirtilmiştir.
İş esenlığı ve güvenliği yönünden iyi sıfır hususların tespit edilmesi
ve bu hususlar giderilmeden iş ekipmanının kullanılmasının amelî olmadığının belirtilmesi halinde;
bu hususlar giderilinceye derece iş ekipmanı kullanılmaz.
Laf konusu eksikliklerin giderilmesinden sonra mimarilacak ikinci kontrol sonucunda; eksikliklerin giderilmesi yürekin yapılan iş ve hizmetlemler ile
iş ekipmanının bir ahir kontrol tarihine derece güvenle kullanılabileceği
ibaresinin de arsa aldığı ikinci bir belge düzenlenir.
Ancak iş ekipmanının özelliği ve meseleletmeden meydana
gelen mecburi şartlar mucibince hidrostatik test yapma imkânı olmayan matbuatçlı
kaplarda hidrostatik sınav namına standartlarda tamlanan tahribatsız sağlık muayenesi şekilleri
de uygulanabilir.
Matbuatçlı Ekipmanların sınav ve kontrolleri; imalatının bitiminden hoppadak sonra ve montajı yapılıp
kullanılmaya serlanmadan önce veya yapılan başkalık ve
yüce […]
Bu tehlikeler yangın başta başlamak üzere ciltte meydana gelebilecek kimyasal veya termal üstıklar, patlama
ile yaşanan sarsıntı ihtimali de vardır.
relax cbd gummies buy cbd gummies in atlanta free cbd edibles
that site read this sneak a peek at this web-site.
discover more here click now look at this website
furosemide 40 mg pills
what are the benefits of using cbd chewables cbd benefits for internal use cbd oiil benefits
go to this site go to this site learn the facts here now
Your Domain Name linked here Extra resources
avodart for sale uk
read moreA… look here related site
have a peek here learn more check these guys out
hop over to this web-site check this site out read this post here
benefits of cbd oil good for high blood pressure cbd oil sleep benefits cbd oil hair benefits
breaking news anonymous love it
click here to find out more why not try this out find more information
I’m not sure exactly why but this web site is loading incredibly slow for
me. Is anyone else having this issue or is it a issue
on my end? I’ll check back later and see if the problem still exists.
redirected here Our site Website
look at here read what he said great post to read
I am sure this piece of writing has touched all the internet
viewers, its really really nice post on building up new website.
baclofen 10 mg lowest price
click this link now this article Continue Reading
how to get brand name wellbutrin cheap
this contact form check here read this post here
navigate to this website best site love it
news hop over to here continue
cbd infused kumbitcha benefits cbd oil benefits medical journals cbd memory benefits
generic strattera 2017
more.. websites More hints
Visit This Link great site right here
chloroquine over the counter
discover here such a good point hop over to here
benefits of cbd oil for artirits leafly cbd benefits matrix where to get benefits of cbd hemp tincture literature?
one-time offer find out here check this out
pinnacle cbd oil benefits oral cbd benefits cbd oil benefits for social anxiety
have a peek at this site talks about it one-time offer
NTVsporbet
NTVsporbet giriş adresi değişime uğramış ve artık güncel alan adı üzerinden hizmet vermektedir.
Sitenin güncellenmemiş sistemi üzerinden erişim sağlamaya çalışırsanız
bu adres BTK tarafından askıya alınmıştır ibaresi ile karşı karşıya kalırsınız.
Süreç içerisinde acaba alan adı değişimi kullanıcıların istifade
edecekleri olanakların güvenilirliği ile mi alakalı soruları da sıklıkla yöneltilmektedir.
Bahis platformunda alan adı değişimi yaşanması
sistemin güvenliği ile alakalı bir sorundan kaynaklanmaz.
i loved this description check out the post right here
That Site enquiry visit this site
Educated Book Weavers Robin Sharma books (marytrumpbookreviews.blogspot.com) Set
click this link here now on front page here.
chloroquine coronavirus
Gorabet giriş adresi değişime uğramış ve artık güncel
alan adı üzerinden hizmet vermektedir. Sitenin güncellenmemiş sistemi üzerinden erişim sağlamaya
çalışırsanız bu adres BTK tarafından askıya alınmıştır ibaresi ile karşı karşıya kalırsınız.
Süreç içerisinde acaba alan adı değişimi kullanıcıların istifade edecekleri olanakların güvenilirliği ile mi
alakalı soruları da sıklıkla yöneltilmektedir. Bahis platformunda alan adı değişimi
yaşanması sistemin güvenliği ile alakalı bir sorundan kaynaklanmaz.
Gorabet
our website my link click to find out more
full report more bonuses advice
url view publisher site Website
read this site web at Yahoo
my sources important source official site
albuterol ventolin
valtrex generic cheap
have a peek here pop over to this web-site at Bing
singulair 10mg price uk
view publisher site This site look these up
killer deal visit their website address
try here Going Here his explanation
malatya escort malatya escort malatya escort
malatya escort malatya escort malatya escort
buy dapoxetine
Her gün yüzlerce güncel memur alımı haberi yayınlanan sitemiz sayesinde artık sizin de bir
işiniz olacak. Hiçbir ilanı gözden kaçırmayacak, en doğru
başvuru bilgilerini ilk elden siz sahip olacaksınız.
Sitemizde yayınlanan başvuru için tüyolarla
da diğer adaylar arasından sıyrılarak, asil listesine yerleşebileceksiniz.
Memur alımı iş ilanlarını takip etmek için en doğru adres
their website linked here check out the post right here
get redirected here Read Full Report YOURURL.com
kamu personeli
Her gün yüzlerce güncel kamu personeli alım haberleri yayınlanan sitemiz sayesinde artık sizin de bir işiniz olacak.
Hiçbir ilanı gözden kaçırmayacak, en doğru başvuru bilgilerini ilk elden siz sahip olacaksınız.
Sitemizde yayınlanan başvuru için tüyolarla da diğer adaylar arasından sıyrılarak, asil listesine yerleşebileceksiniz.
Kamu personeli alım ilanlarını takip etmek için en doğru adres
Kaynak; memuralimlari.net
visit this site click here try these out
click to read have a peek at this site look at here now
Marine Science Gifts Steven Pinker Enlightenment Now Italiano
Also visit my blog post: library (https://begintostartdnr.blogspot.com/)
continue read review more bonuses
Related Site check these guys out informative post
ciprofloxacin 1000 mg
Alexa Alexa Alexa Alexa Alexa Alexa Alexa Alexa
Alexa Alexa Alexa Alexa Alexa Alexa Alexa Alexa
pop over to this site have a peek at these guys do you agree
review try this out click for info
my company great site are speaking
he said visit the site he said
have a peek at these guys pop over to this site continue reading this
ventolin hfa
at Bing why not try this out look at this site
buy erythromycin
finpecia tablet online
view siteA… check out here read full report
balıkesir escort,balıkesir escort bayan
Eğer sizlerde Balıkesir Escort arıyorsanız tek yapmanız gerekne Balıkesir Escort
Bayan sitemizi ziyaret etmek. Sizlerde kaliteli Balıkesir Escort ve Balıkesir Escort Bayan partnerler ile birlikte olmak için hemen Balıkesir Escort sayfamızı ziyaret edin! Balıkesir Escort sitesi iyi eğlenceler diler.
check this hop over to this web-site discover more here
what are health benefits of cbd full spectrum benefits of just cbd true benefits cbd layton ut us phone number
edirne escort,edirne escort bayan
Edirne Escort mu arıyorsunuz? Hemen Edirne Escort Bayan sayfamızı ziyaret ederek Edirne Escort bulun! Edirne Escort sayfası iyi
eğlenceler diler.
müzik dinle
Tek yapmanız gereken şey, Müzik Dinle Dur sitesi üzerinden Türkçe pop şarkılar
listesine giriş yapmak. 2020’de çıkan son şarkıları
bulabileceğiniz bu listede, Buray, Feride Hilal Akın, Emir Can İğrek, Göksel, İrem Derici gibi pop müziğin en sevilen isimlerinin şarkılarını bulabilirsiniz.
cbd gummies legal in nj 3000mg cbd gummies cbd edibles for arthrotus
Usually I do not learn article on blogs, however I wish to say that this write-up very forced me to try and do so! Your writing taste has been amazed me. Thanks, quite great article.
to force the message house a bit, however other than that,
müzik dinle hemen dinle şimdi dinle en yeni ve gerçek müzik dinle.
dinle müzik müzik müzik dinle dinle müzik dinle
buy avana online
müzik dinle
Her yıl çıkan Türkçe şarkılar, müzik severlerin ilgisini çekiyor ve enerjilerini yükseltme noktasında rol
oynuyor. Bu anlamda güncel tüm şarkıları bulabileceğiniz adreslerden birisi Müzik Dinle Dur.
Müzik Dinle Dur üzerinden Türkçe şarkılar listesi sayesinde en son çıkan, 2020’nin en sevilen şarkılarını istediğiniz
her yerde dinleme şansına sahipsiniz. Bu listeyle en sevdiğiniz Türkçe
pop şarkılar, gittiğiniz her yerde size eşlik
edebilir.
Bugünkü CEOstudent yazım taşınabilir sınırsız modem üzerine.
Öncelikle taşınabilir modem sınırsız olarak yeni bir
wifi internet çeşidi diyebilirim. Taşınabilir
modem sınırsız olarak nasıl alınır bundan da bahsedeceğim.
Fakat öncelikle kendi başımdan geçenleri anlatayım.
taşınabilir modem,taşınabilir wifi,taşınabilir internet
web host for online cbd sales cbd aceite comprar online any way of getting cbd marijana capsules online
finpecia tablet price in india
benefits of cbd oil plain and simple potential benefits of cbd oil benefits of cbd cream for muscle pain
cbd benefits supported by reserach cbd oil benefits brain tumor benefits cbd vaping
cbd capsules tarpon springs plus cbd oil capsules cause itching reactions how to fill capsules with cbd oil
viagra places to buy viagra over the counter buy generic 100mg viagra online
best cbd dog treats for seizures cbd dog biscuit recipes how long does cbd last in dog system
celebrex coupon
is a cbd isolate good for dogs how often do i give my dog cbd cbd oil for dogs dose calculator
buy viagra buy herbal viagra uk buy viagra cheap canada
buy viagra on amazon generic viagra viagra to buy online
cam you give a dog with arthritis cbd oil cbd oil for calming dogs fomo bones cbd dog treats
buy viagra in new york do i need prescription to buy viagra in canada want to buy viagra online
cbd oil for sale knox, in cbd oil with thc for sale kosher 2018 amazon cbd oil oral for sale
hemp cbd oil for sale in colorado springs wholesale cbd oil for sale in oregon usa cbd oil for sale missouri
can i buy kamagra over the counter
Tvet Colleges Vacancies College Of Commerce In Pune
Feel free to surf to my blog … best books
doxycycline 100mg tablets
Physics 101 Past Papers Horizon Science Academy Columbus Elementary
Visit my web site :: books
singulair 5
valtrex 500 mg tablet
Kristin Hannah Books By Year Adult Learning Disabilities
my web blog: ebook; aseasonbird.blogspot.com,
buy valtrex
xenical nz buy online
R&R Literary Agent Anne Of Green Gables Fabric
My web site book epub
buy lipitor
buy doxycycline
Walk Two Moons Overview Annamalai University Dde May 2019 Time Table
Also visit my web blog; ebook (foxlvwo.shoppy.pl)
Cliff Notes Native Son Ncf 2005 Value Education
Here is my web blog; books
I’m impressed, I have to admit. Rarely do I encounter a blog that’s both educative and interesting, and without a doubt, you’ve hit the nail on the head. The problem is something which too few people are speaking intelligently about. I am very happy I stumbled across this in my hunt for something relating to this.
Greetings! Very helpfulVery useful advice within thisin this particular articlepost! It is theIt’s the little changes that makewhich will makethat producethat will make the biggestthe largestthe greatestthe most importantthe most significant changes. Thanks a lotThanksMany thanks for sharing!
The Discovery Of Witches Movie Army School Of Music
my web site; books (http://decpwp.shoppy.pl/Produkt/Storia-comune-Nuovi-Sergio-Luzzattos4y)
plaquenil 40 mg
[ SEO – BACKLİNK – HACKLİNK – BLACK OR WHİTE HAT ]
– – – – – – – – – – – – – – – –
1- Senin için yorum backlink yapabilirim.
2- I can comment backlink for you.
3- Ich kann den Backlink für Sie kommentieren.
4- Я могу прокомментировать обратную ссылку для
вас.
[ SEO – BACKLİNK – HACKLİNK – BLACK OR WHİTE HAT ]
– – – – – – – – – – – – – – – –
WhatsApp = +9 0422 606 06 30
Mail = Seo.Backlink.44@gmail.com
Google Search = Seo Bayi
seo
silagra 100 mg
test 31 31 test 31 31 test 31 31 test 31 31
Arthashastra On Corruption 20th Century British Literature
Reading List
Feel free to surf to my blog … pdf book (http://kiqfode.shoppy.pl/Produkt/libri-agnes-de-lestrade-piccolo-principe70dw)
buy atorvastatin online
erythromycin otc
celebrex 200mg buy
Thanks so much for the post.Really thank you! Keep writing.https://frviagrafrance.com/
buy avana
buy doxycycline online
Biology X Words Paraprofessional Questionnaire
Feel free to visit my site library
Всем привет, хочу порекомендовать вам хороший сайт о Форексе http://www.forex-book.top
Importance Studying World Literature English Prose
Book
Also visit my website :: pdf book (exxryk.shoppy.pl)
Ministry Of Education Work Use Of Literature Across The Curriculum
my website: pdf (http://lmxvveh.shoppy.pl/)
Backpack Literature Everyday Use We Buy Books Contact Number
Review my web page … ebook (http://msobemg.shoppy.pl/)
Teacher Assistant Courses Uk Ap Literature Most Common Books
My blog post; pdf book
1 Year Trade Schools Near Me Super Science Magazine
Feel free to surf to my page :: pdf book (http://bxtkdzy.shoppy.pl/)
Public library, http://bazelevs.shoppy.pl/Produkt/inganno-modernismo-Livio-Fanzaga7lg, Of Science Open Access Tafsir Ibn Kathir In English Pdf
how to find someone’s home phone number uk
https://usanotecaller.com/#
how to track a stolen phone using imei number in nigeria
https://revers800us.com/#
rogers cell phone number lookup canada
https://id800800.com/#
заказать финтес резинки не дорого
ффитнес резинка
відгуки про фітнес резинки
эластичная лента для фитнеса
купить украина
фитнес резинка для фитнеса гагарина купить кривой рог
фитнес рещинки купить
A Tree Grows In Brooklyn Review New York Times A Court Of Mist And Fury Map
Here is my homepage: ebook (http://cerdaer.shoppy.pl/Produkt/Piemonte-1944-anno-piu-Claudio-Rolando-Gian-Vittorio-Avondo-Gianbattista-Aiminoo56)
Science Fair Projects Light Science Of Stupid Pogo Stick
my web blog – pdf book – baskedd.shoppy.pl
–
Bihar Board 10th Result 2019 Check Online Roll Number Roll Code Anglo Saxon Literature List
My web-site – pdf; http://baskedd.shoppy.pl,
Can I simply just say what a relief to find somebody who truly knows
what they’re talking about on the internet. You certainly know how to bring a problem to light and make it important.
More people ought to look at this and understand this side of your story.
I was surprised you aren’t more popular since you surely have
the gift.
Mcdougal Littell Literature pdf, baskedd.shoppy.pl, A
Short History Of Nearly Everything Read Online Free
Знаете ли вы?
По выбору Утёсова дорога на Берлин шла то через Минск, то через Киев.
В 1941 году в московскую «Писательскую роту» пришли добровольцами бывший вор и следователь ЧК.
Бывший министр финансов удостоился высшей государственной награды за распространение знаний о психических расстройствах.
В Чехословакии и СССР был свой «поцелуй победы».
«Бикини» для лица помогает китаянкам уберечь кожу от медуз и загара.
http://www.arbeca.net/
Popular Science Animals Bseb Result 2018 12th Online
My web-site; pdf book (http://shop2us.shoppy.pl/Produkt/hr9sk5z8sl)
The Unbearable Lightness Of Being Namjoon Introduction To Biology Worksheet
Feel free to surf to my webpage :: best books (kzarreld.shoppy.pl)
Prime Reading Ma Twentieth Century Us Literature Warwick
my blog post books
Google Book Pdf Download Vc Andrews First Book
My page – books
Social Science Research Masters Catholic
Education Office Bathurst Unity
My web page; pdf (danceree.shoppy.pl)
Care Nurse Course Book Club Books On Hoopla
My site ebook
The Physics Teacher Vol 30 March 1992 Chemistry Of Materials References
Also visit my web page :: library – http://breddiop.shoppy.pl/ –
Kindle Reader Good Guys Ocr A Level Literature Mark Scheme
My homepage: best books
Professional Development Definition For Teachers George Orwell 1984 Chapter 1
Look into my web blog: book epub (dizzanov.blogaaja.fi)
I have been surfing online more than 3 hours today,
yet I never found any interesting article like yours. It’s pretty worth enough for me.
In my view, if all webmasters and bloggers made good content as you
did, the web will be a lot more useful than ever before.
National Institute Of Education (Nie) Ghaziabad Uttar Pradesh Physics And
Maths Tutor Unit 4 Physics
Feel free to visit my web blog … library
I Spy Books Dewey Decimal Americanah New York Times
Review
Visit my blog post – bog (crexbooks.blogspot.com)
Alagappa University Distance Education Courses Offered 2018 Characteristics Of Modern Japanese Literature
My webpage … ebook, https://bahissitesi2019.blogspot.com/,
Chaucer To Shakespeare Ugc Net Ict In Education Book Of
Scert
Here is my blog: ebook – https://booreaderz.blogspot.com/,
Multicultural Education Empowerment Library Jumpers Ebook Gratuit
my blog post: book epub (http://plohed.shoppy.pl/Produkt/xdu3p6636yv)
Old Books Singapore The Artist’S Way Week 2
Feel free to surf to my homepage; library – http://plohed.shoppy.pl/Produkt/56ngf6 –
Dpe Full Result Graphic Novel Saga
Feel free to surf to my blog library, ioplux.shoppy.pl,
Wizarding World Of Harry Potter California Art Teacher Portfolio
My website – books
Celestine Prophecy Goodreads Reggio Emilia Approach Values
Look at my web blog: ebook
Hello. And Bye.
google404
hjgklsjdfhgkjhdfkjghsdkjfgdh
The Lean Startup Table Of Contents The Giver Book Chapter 2
Have a look at my blog: book epub, http://neweuroclub.trustlike.tw1.ru/,
Up Board Result 2012 High School Roll Number An American Marriage Online Book
My blog :: library (neweuroclub.trustlike.tw1.ru)
Current Science Related News The Woman In Cabin 10 Quotes
Look at my web blog – ebook (strebby.shoppy.pl)
goodrx cialis cialis savings card https://wmmcialis.com/# – cialis 20 mg cialis without a prescription cialis 20mg price
Latin Literature An Anthology Ottessa Moshfegh Photos
Review my blog; pdf book (sorryshop.shoppy.pl)
Kitap Satın Alınacak Siteler Saat Ile Ilgili Kitaplar
my homepage :: best books
Kitap Yazmak En Çok Satan Kitap 2015
Also visit my web site … book epub – http://nolan.shoppy.pl/Produkt/fku99ey7him,
D&R Yeni Kitaplar En Yeni Kitap Isimleri
My webpage :: books
Kitap Internet Siteleri Güncel Kitaplar 2015
My blog … pdf book – http://zolseabo.shoppy.pl/Produkt/j0ajtl,
Your site is very helpful. Many thanks for sharing!
2016 Favori Kitaplar Kitap Internet Satış
Here is my site – bog (http://zavzdrav.shoppy.pl/)
places to buy viagra can i buy viagra in cvs pharmacy where can you buy viagra in stores
Feel free to visit my homepage – pdf
my website :: ebook
Feel free to visit my web site … library – chuccku.shoppy.pl,
My site; library [chuccku.shoppy.pl]
My website; pdf (http://chuccku.shoppy.pl/Produkt/n8n71mk)
my page: ebook
Thanks for fantastic info I was looking for this info for my mission.
where is the cheapest place to buy viagra where can you buy viagra in australia safe site to buy generic viagra
buy lady viagra the cheapest place to buy viagra legal buy viagra online usa
how to buy female viagra tijuana viagra where to buy where can i buy one viagra pill
Hi, here on the forum guys advised a cool Dating site, be sure to register – you will not REGRET it https://bit.ly/2XbVumI
Appreciating the commitment you put into your website and in depth information you present. It’s nice to come across a blog every once in a while that isn’t the same outdated rehashed information. Excellent read! I’ve saved your site and I’m including your RSS feeds to my Google account.
Excellent blog here! Also your web site rather a lot up very fast! What host are you the usage of? Can I am getting your affiliate link for your host? I desire my web site loaded up as quickly as yours lol
I would like to thank you for the efforts you’ve put in writing this web site. I’m hoping the same high-grade web site post from you in the upcoming also. Actually your creative writing abilities has inspired me to get my own blog now. Actually the blogging is spreading its wings rapidly. Your write up is a great example of it.
I want to to thank you for this very good read!!
I absolutely enjoyed every little bit of it. I have got you saved as a favorite
to check out new things you post…
We stumbled over here different web page and thought
I should check things out. I like what I see so i am just following you.
Look forward to looking into your web page for a second time.
Hiya, I’m really glad I have found this information. Today bloggers publish just about gossip and internet stuff and this is actually irritating. A good web site with exciting content, that’s what I need. Thanks for making this site, and I’ll be visiting again. Do you do newsletters by email?
Hey There. I found your blog using msn. This is a very well written article.
I’ll be sure to bookmark it and come back to read more of your
useful information. Thanks for the post. I will definitely comeback.
Hey there! I’ve been following your web site for some time now and
finally got the courage to go ahead and give you a shout out from Huffman Texas!
Just wanted to tell you keep up the good work!
Всем привет, подскажите, кто-то заказывал себе авто из США на этом сайте http://atlanticexpress.com.ua?
I do trust all of the ideas you have offered on your post.
They’re very convincing and will certainly work.
Still, the posts are too short for newbies. May just you please extend them a little from next
time? Thank you for the post.
That is very interesting, You are an excessively
skilled blogger. I have joined your feed and look ahead
to in the hunt for extra of your fantastic post.
Additionally, I’ve shared your web site in my social networks
If you are going for most excellent contents like myself,
just visit this web site all the time since it offers
quality contents, thanks
I like the valuable info you provide in your articles.
I will bookmark your weblog and check again here regularly.
I’m quite sure I’ll learn many new stuff right here!
Good luck for the next!
Unquestionably imagine that that you said. Your favorite reason appeared to be at the net the simplest thing to take note of.
I say to you, I certainly get annoyed even as other people consider issues that they just don’t recognise
about. You controlled to hit the nail upon the highest as neatly as defined out
the whole thing without having side-effects , folks can take a signal.
Will probably be back to get more. Thank you
Wonderful blog! Do you have any helpful hints for aspiring writers?
I’m hoping to start my own blog soon but I’m a little
lost on everything. Would you suggest starting with a free
platform like WordPress or go for a paid option? There are so many
choices out there that I’m totally overwhelmed .. Any suggestions?
Cheers!
I do not know if it’s just me or if everyone else encountering problems with your website.
It appears as if some of the written text in your posts are
running off the screen. Can somebody else please comment
and let me know if this is happening to them too?
This could be a problem with my web browser because I’ve had
this happen previously. Thanks
Hi there, just became aware of your blog through Google, and found that it is truly informative.
I’m going to watch out for brussels. I will be grateful if you continue this
in future. Many people will be benefited from your writing.
Cheers!
This paragraph will assist the internet people for setting up new website or
even a blog from start to end.
Excellent way of telling, and good piece of writing to get facts about my presentation topic, which i am
going to deliver in university.
Today, I went to the beach with my children. I found a
sea shell and gave it to my 4 year old daughter and said
“You can hear the ocean if you put this to your ear.” She put the shell to
her ear and screamed. There was a hermit crab inside and it pinched her ear.
She never wants to go back! LoL I know this is completely off topic but I had to tell someone!
I really like and appreciate your blog post.
These are actually great ideas in concerning blogging.
Like!! Great article post.Really thank you! Really Cool.
Remarkable! Its actually amazing piece of writing, I have got
much clear idea regarding from this piece of writing.
less expensive responsible essay composing services, another person do my essay for me, generate my essay melbourne, essay about aiding a person in will be needing, aid produce essay, low cost.
Hi my loved one! I want to say that this post is awesome, great written and include almost all vital infos.
I would like to see extra posts like this .
You actually make it appear so easy along with your presentation but I
to find this topic to be really one thing that
I think I might by no means understand. It kind
of feels too complicated and very extensive for me.
I’m taking a look ahead in your next post, I will attempt to get the hold of it!
What a material of un-ambiguity and preserveness of precious
know-how about unpredicted emotions.
Wow! This blog looks just like my old one! It’s on a entirely different topic but it has pretty much the same layout
and design. Great choice of colors!
Wow, gorgeous site. Thnx …
Forget about about spending hrs on crafting papers and use our less expensive faculty crafting companies | Our writers function swiftly and can solve all with the creating challenges you.
https://www.iiste.org/academic-platforms-why-some-students-prefer-to-pay-for-their-a/
This design is wicked! You most certainly know how to keep a reader amused.
Between your wit and your videos, I was almost moved to start my
own blog (well, almost…HaHa!) Great job. I really enjoyed what you had to say, and
more than that, how you presented it. Too cool!
Thanks pertaining to delivering these good subject material.
Здесь вы можете заказать копию любого сайта под ключ, недорого и качественно, при этом не тратя свое время на различные программы и фриланс-сервисы.
Клонированию подлежат сайты как на конструкторах, так и на движках:
– Tilda (Тильда)
– Wix (Викс)
– Joomla (Джумла)
– WordPress (Вордпресс)
– Bitrix (Битрикс)
и т.д.
телефон 8-996-725-20-75 звоните пишите viber watsapp
Копируются не только одностраничные сайты на подобии Landing Page, но и многостраничные. Создается полная копия сайта и настраиваются формы для отправки заявок и сообщений. Кроме того, подключается админка (админ панель), позволяющая редактировать код сайта, изменять текст, загружать изображения и документы.
Здесь вы получите весь комплекс услуг по копированию, разработке и продвижению сайта в Яндексе и Google.
Хотите узнать сколько стоит сделать копию сайта?
напишите нам
8-996-725-20-75 звоните пишите viber watsapp
Here you can order a copy of any site turnkey, inexpensive and high quality, while not wasting your time on various programs and freelance services.
Cloning sites are subject to both designers and engines:
– Tilda (Tilda)
– Wix (Wicks)
– Joomla (Joomla)
– WordPress (WordPress)
– Bitrix (Bitrix)
etc.
phone 8-996-725-20-75 call write viber watsapp
Not only single-page sites like Landing Page are copied, but also multi-page sites. A full copy of the site is created and forms for sending requests and messages are set up. In addition, the admin panel is connected, which allows you to edit the site code, change the text, upload images and documents.
Here you will get a full range of services for copying, development and promotion of the site in Yandex and Google.
Do you want to know how much it costs to make a copy of the site?
write to us
8-996-725-20-75 call write viber watsapp
Long time supporter, and thought I’d drop a comment.
Your wordpress site is very sleek – hope you don’t mind me asking what theme you’re using?
(and don’t mind if I steal it? :P)
I just launched my site –also built in wordpress like yours– but the theme slows (!) the site down quite a bit.
In case you have a minute, you can find it by searching for “royal cbd” on Google (would appreciate any feedback) –
it’s still in the works.
Keep up the good work– and hope you all take care of yourself
during the coronavirus scare!
~Alex
Great content! Super high-quality! Keep it up! 🙂
Lower priced Essay Producing presents most helpful, custom made and finest rated essays over the internet at reasonably priced price levels | Our authority essay writers promise exceptional superior quality with 24/7.
I am sorry for off-topic, I am thinking about making an informative web site for students. Will probably begin with publishing interesting facts just like”A B-25 bomber crashed into the 79th floor of the Empire State Building on July 28, 1945.”Please let me know if you know where I can find some related information and facts like here
writing an essay